はずる

はじめに

この記事はこの記事はプログラミングラボ部アドベントカレンダー趣味部門 16日目の記事として書かれています

https://adventar.org/calendars/4410

昨日はしのさんの記事でした。趣味アドカレっていろんな人のことが知れていいですね。

最近気づいたことなんですがアドカレって結構かくの時間かかるんですね。

はずる

これは正真正銘僕の趣味なんですが、はずるというパズルシリーズがあります。

www.hanayamatoys.co.jp

いわゆる「知恵の輪」と呼ばれるやつです。昔はキャストパズルという名前でした。おもちゃ屋さんとかでお試しが置いてあるのを見たことがある人も多いのではないのでしょうか？一昨年あたりにはよく学校に持ってきてカチャカチャやっていた気がします。結構前からちょくちょく買っていて、今家に20個くらいあります。今回はそんなはずるの魅力について語っていきたいと思います。

見た目が美しい

はずるのパズルはすべて金属でできていて、デザインも凝っているものが多いのでとても美しいです。僕のMisskeyのアイコンもはずるのパズルにしています。美しいですね。

キャストヴォルテックス(僕のアイコン)
f:id:Unit112358:20191216175120j:plain

キャストハーモニー デザイン性がよい
f:id:Unit112358:20191216175329p:plain

パズルとしても楽しめますが、部屋において眺めるだけでも楽しいです。もし購入を検討する場合は見た目で決めてしまうのもいいかもしれません。

難易度が細かく分かれている

はずるは難易度1から難易度6までの6段階の難易度があり、パズル初心者でも安心して遊ぶことができます。とはいっても難易度1が簡単すぎるということはなく、低難易度でも頭を使わないと解けないものが多いです。難易度一の中で最もおススメできるはずるを貼っておきます。

キャストダイヤモンド
www.hanayamatoys.co.jp
f:id:Unit112358:20191216180437p:plain

難易度1ですが結構頭を使いました。解けたときの驚きと意外性も十分なので、最初に手を出すのには最適なパズルです。

意外性

ジグソーパズルやペンシルパズルと違って、はずるは知恵の輪なので三次元的な動かし方ができます。いろんな動かし方を考えながらカチャカチャやっていると、予想もできないような動きをすることがありとても面白いです。他のパズルのようにただ考えるだけではなく、意外性のあるパズルなので何度も遊びたくなります。

耐久性に優れている

はずる以外のパズルでもよく遊ぶのですが、木製のパズルだと破損してしまったり温度によって膨張してしまったりすることがあり、本来の面白さが失われてしまう可能性があります。前述したとおりはずるは金属でできているため、曲がったりつぶれたりして遊べなくなってしまうことが少ないです。長く安心して遊ぶことができます。だからといって乱暴に扱っていいというわけではないですけどね。

おわり

どうでしょうか？面白そうですよね。値段は少々高めですが、それににあう面白さがあると思います。もしどこかで売られているのを見かけたら買ってみてください。

明日は現部長の記事です。何について書くのか楽しみですね。

#define int long long

はじめに

この記事はこの記事はプログラミングラボ部アドベントカレンダープロ部門 11日目の記事として書かれています。

https://adventar.org/calendars/4410

昨日の記事は面白かったですね。超絶大事ではない話をします。

競技プログラミング

僕の2年生までの部活動はすべて競技プログラミングでした。3年生になってからは本格的にすることは少なくなりましたが、毎週コンテストの問題を見て考察するくらいはしていました。いくつか大会にも出ています。まとめると結構長い時間競技プログラミングをやっていたということです。

そんな僕が最近知った非常に便利なマクロがあります。それがこちら、

#define int long long

長い時間競技プログラミングをやっていた僕が最近知ったので、おそらくこの記事を読んでいる人たちは知らないんじゃないですかね。今回はこの便利なマクロについて話していこうと思います。

何がうれしいか

競技プログラミングで出題される問題には、int型に格納できる値より大きい値を扱わないといけないものがあります。数え上げとかがそうですね。その場合、int型の代わりにlong long型というものを使う必要があるのですが、このマクロを使うことでintと書くとlong longとみなしてくれるようになります。桁あふれを気にしなくてよくなるわけですね。

こんなに便利なんだから何かデメリットがあるかと思ったら特にないんですよね。1つは

int main(void)

を

signed main(void)

と書かないといけなくなることです。めんどくさいですが慣れればデメリットでもなんでもないですね。あとは、少しだけ実行時間が伸びてしまうことなんですが、そのせいでTLEが出たみたいな話はほとんど聞かないので(全くないわけではない)、気にしなくていいと思います。

おわり

こんな感じで便利なのでみんな使おう。

明日ははと君の記事です。「うわぁぁぁぁぁぁぁぁぁぁぁ」と書いてありますが何の記事を書くんでしょうか？

おまけ

このままだと情報量0なので、なんで#define int long longについて書いたかを話します。

この前ICPCという大会に出ました。結果は下から1/4くらいだったと思います。

問題が結構多く、最初の2問だけ難易度順に並んでいるので、まずははじめの2問を解いてから簡単な問題に取り掛かるというのが基本的な戦術だと思います。僕たちのチームも同じ戦術をとりました。

Bがすごく簡単だったのに対し、A問題が意外に難しくて少し時間がかかったのですが、何とかAとBを通してほかの問題を解き始めました。ちなみに問題文の英訳はchocobo333とgedorinku先輩がやってくれました。僕は英語ができないのでかなり助かりました。

明らかに難しそうな問題でなく、他のチームが多く解いている問題だったのでH問題に手を付けることにしました。適当に考察していると解法っぽいものが浮かんだので実装開始、数分後に嘘だとわかったので考察しなおし、今度こそは解法が浮かんだので実装再開、みたいな流れだったと思います。

とりあえず実装が終わってサンプルも通ったので提出。WA
えーなんでーとか思いながらデバッグ。20分くらいでバグがわかりなおして提出。WA

ここから何が間違っているのか分からないまま、コードを眺めたり自作サンプルを試したりする時間が一時間くらい続きました。実装をしたのが久しぶりだったので超難解なコードを書いてしまい、僕以外デバッグできないみたいになって最悪でした。

一時間くらいがたったくらいでgedorinku先輩が「これ最大ケースでオーバーフローするくない？」みたいなことをつぶやきました。僕は頭が真っ白になりました。intをlong longに変えて提出。AC

残り時間1時間くらいだったのでとりあえず考察を始めたのですが、あまり集中できずにそのまま大会終了。悲しいですね。

正直、#define int long long をはじめから書いていたからといって正解数が増えていたことはないと思いますが。チームメンバーに迷惑をかけてしまったのでかなり反省しました。この経験で「これからのコードは絶対に#define int long longを書くぞ」と誓いました。二回目ですけどね、これを誓ったのは。というわけで、皆さんも#define int long longをしましょうね。

おまけ2

久しぶりに競プロをしたので最近思っていることを話します。僕が一番競技プログラミングを楽しんでいたのは、おそらく初めてすぐか、JOI非公式難易度表の10くらいを埋めているときだったと思います。初めたばかりのころは、自分が考えた通りにプログラムが動くのがただただ楽しくて競プロをしていました。10を埋めている頃は、何とか自力で解ける難易度の問題を解くのが楽しかったですね。ただ、そのころから考察に対して実装が重くなってきたと感じることが多くなりました。考察をしているときは楽しいのですが、それを実装に移そうとすると面倒くさくて次の問題の考察に移ってしまう、ということもしばしばありました。実装して初めて自分の考えがあっているのかがわかるというのに...。ちなみに考察より実装が重いと思っていたのは僕だけではなく、某先輩も同じことを思っていたそうです。

当時はそんなことを考えていたのですが、最近は考え方が変わってきていています。アルゴリズムを考えることも大切だけど、うまい実装法を考えることこそが、競技プログラミングに求められていることなのではないか、みたいな感じに変わってきています。実際、強い人のコードはシンプルで短く読みやすい印象があります。しばらく競技プログラミングをすることはないと思いますが、また競技プログラミングを始めることがあれば、ここら辺を頭において精進しようと思っています。

僕の夢

はじめに

この記事はプログラミングラボ部アドベントカレンダープロ部門 9日目の記事として書かれています。

https://adventar.org/calendars/4410

8記事中4記事書き終わりました。この記事は5記事目です。

僕の夢

皆さんは「癒されたい」と思ったときどんなことをしますか？

僕は家に水生生物を何種類か飼っているので、癒されたいときは彼ら(性別知らんけど)を見て癒されています。かわいいですね水生生物。

ただ、頻繁にみているとさすがに飽きてきてしまいます。かわいいのは変わりないのですが、たまには違う種類の水生生物を見たいなーと思うことがあります(ちなみに僕は水生生物を除いた動物の容姿があまり好きではありません、植物は好きです)。

そんなことを思っているうちに、自分で生体シミュレーションができるプログラムを作ればいいのでは？みたいなことを思いつきました。勝手に進化して生物の動き方や性質が変われば飽きることもないし、見た目も自分好みにできるし、無限に癒されることができそうみたいなのりです。

とはいっても、どんなものにするのかもほとんど決まっていないので、いつか作れればいいなーというのが僕の夢です。しょぼい夢ですね。

本題

自分の夢を語るだけでプロラボのアドベントカレンダーが務まるとは思っていません。ここからが本題です。

生物シミュレーションをするにあたって、いろいろなことを調べているうちに、Boidsアルゴリズムなるものがあることを知りました。これは、動物の群れをシミュレートするアルゴリズムで、映画などに出てくる鳥や魚の群れを本物と同じように動かすために活用されています。

アルゴリズム

Boidsアルゴリズムは、以下の3つのルールを各生物に対して適用するだけで、群れのような動きを実現することができます。

分離(Separation)

一定範囲にいる他の生物から離れるような方向に動かす。
f:id:Unit112358:20191208232444p:plain

整列(alignment)

一定範囲にいる他の生物が向いている平均の方向を向くように動かす。
f:id:Unit112358:20191208232448p:plain

結合(cohesion)

一定範囲にいる他の生物の平均位置の方向に移動する。
f:id:Unit112358:20191208232453p:plain

たったこれだけで群れのような動きを実現できます。

下のサイトで実際にどのように動くかを見ることができます。

Flocking boids - bl.ocks.org

かわいいですね。
結構簡単に実装できるので、興味がある人は自分で作ってみてください。

おわり

明日はchocobo333の記事です。多分遅刻するんじゃないですかね。

やわらかい幾何学３

初めに

この記事はプログラミングラボ部アドベントカレンダーおかわり部門 8日目の記事として書かれています。

adventar.org

8記事も書くのきつすぎ。

「やわらかい幾何学２」の続きです。

前回の復習

はしませんが、前回計算した境界作用素やその他もろもろを貼っておきます。

図形のKさん
f:id:Unit112358:20191205010628p:plain

図形のKさん(向き付けあり)
f:id:Unit112358:20191205010632p:plain

境界作用素の方々

\partial_2 = \begin{pmatrix} 0 \\ 0 \\ 1 \\ -1 \\ 1 \\ 0 \\ 0 \end{pmatrix}

\partial_1 = \begin{pmatrix} -1 & 1 & 0 & 0 & 0 & 0 & 0 \\ 1 & 0 & -1 & -1 & 0 & 0 & 0 \\ 0 & -1 & 1 & 0 & -1 & -1 & 0 \\ 0 & 0 & 0 & 0 & 0 & 1 & -1 \\ 0 & 0 & 0 & 1 & 1 & 0 & 1 \end{pmatrix}

\partial_0 = \begin{pmatrix} 0 & 0 & 0 & 0 & 0 \end{pmatrix}

サイクル

前回の記事で境界作用素を定義することができました。これを使って、穴の個数を数えてみましょう。

穴はどのような特徴を持っているでしょうか？Kを見ながら考えてみましょう。Kには、e_1、e_2、e_3で作られる穴と、e_5、e_6、e_7で作られる穴の2つの穴があります。これらの穴はどちらも辺に囲まれています。穴であるためには、辺にぐるっと一周囲まれている必要があるようですね。さて、この性質に似たようなことを、前にもどこかで聞いたことがありませんか？前回の記事、「やわらかい幾何学２」の境界の説明のところで、「それぞれの1単体をつなげると、ある方向にぐるっと一周するわっかになる場合、その境界は打ち消しあって0になります」という説明をしました。先ほどの穴も、囲んでいる辺に符号をつけて向きを適切にそろえれば、ぐるっと一周するわっかを作ることができます。

f:id:Unit112358:20191207230515p:plain

さて、ぐるっと一周するわっかの境界は0になるのでした。逆に言えば、\partial_1によって0に移るようなベクトルは、すべてわっかを表現しているといえます。そのようなベクトルの集合はまさに\partial_1の核、すなわち\ker \partial_1です。つまり、穴になるようなベクトルの集合は\ker \partial_1の要素であるといえるわけです。これは\partial_1以外の境界作用素でも考えることができ、\ker \partial_kのことをkサイクルといい、Z_k(K)で表します。

では、先ほど作った\partial_1から、\ker\partial_1を求めてみましょう。計算は省きますが、以下のようになります。

\ker\partial_1 = \biggl<\begin{pmatrix}1 \\ 1 \\ 1 \\ 0 \\ 0 \\ 0 \\ 0 \end{pmatrix},\begin{pmatrix}0 \\ 0 \\ 1 \\ -1 \\ 1 \\ 0 \\ 0 \end{pmatrix},\begin{pmatrix}0 \\ 0 \\ 0 \\ 0 \\ 1 \\ 1 \\ -1 \end{pmatrix} \biggr>

この3つのベクトルの線形結合であらわされるベクトルはすべて穴となるのですが、このままだと少し問題があります。以下の2つの例を見てみましょう。

まずは1つ目の例です。

\begin{pmatrix}1 \\ 1 \\ 1 \\ 0 \\ 0 \\ 0 \\ 0 \end{pmatrix} - \begin{pmatrix}0 \\ 0 \\ 1 \\ -1 \\ 1 \\ 0 \\ 0 \end{pmatrix} + \begin{pmatrix}0 \\ 0 \\ 0 \\ 0 \\ 1 \\ 1 \\ -1 \end{pmatrix} = \begin{pmatrix}1 \\ 1 \\ 0 \\ 1 \\ 0 \\ 1 \\ -1 \end{pmatrix}

これを図で見てみると以下のようになります。

f:id:Unit112358:20191207231211p:plain

これは穴といえるのでしょうか？確かに境界は0になりますが、二つの穴を含んでしまっています。穴の個数を数えるときに、これを1つの穴とみなしたりはしませんね。複数の穴を足し合わせて作られた穴は、穴としてみなすべきではないようです。では、どのように穴を数えればいいのでしょうか？いくつかの穴をつなげたものが穴ではないのなら、ほかの穴をつなげても作ることができない穴こそが、本当の穴といえるでしょう。このような穴の個数は、\ker\partial_1の基底の数と一致します。穴の個数を調べるには、かわりに基底の個数を調べればいいことになります。

しかしこれでも問題は残ります。\ker \partial_1の基底の個数は3個でした。上の考えによると、穴の個数は3個のはずです。これに対して、Kには二つしか穴がありません。これはなぜなのでしょうか？2つ目の例を見てみましょう。

\begin{pmatrix}0 \\ 0 \\ 1 \\ -1 \\ 1 \\ 0 \\ 0 \end{pmatrix}

2つ目の基底を単独で取り出した場合です。図で見てみると以下のようになります。

f:id:Unit112358:20191207231334p:plain

確かにぐるっと一周しているようですが、f_1にふさがれていて穴が消えてしまっていますね。これは穴として数えるべきではないでしょう。このようなものをどうやって数えないようにすればいいのでしょうか？その方法は次のバウンダリーで説明しましょう。

バウンダリー

f_1にふさがれている穴はを囲んでいる辺たちはどのような性質を持っているでしょうか？f_1にふさがれている穴を囲んでいるということは、別の言い方をすればそれらの辺はf_1を囲んでいるといえます。これもどこかで聞いたことがある性質ですね。「やわらかい幾何学２」の境界の説明のところで、「ある鎖群の要素を囲んでいる単体に、適切に+か−をつけて足し合わせて作られる鎖群を、元の鎖群の境界という」という説明をしたと思います。つまり、f_1にふさがれている穴を囲んでいる辺たちは、f_1の境界であるといえます。

f:id:Unit112358:20191207232141p:plain

Kには面がf_1の一つしかありませんが、もっとたくさんの面を持つ図形の場合、それぞれの面から計算できる境界が囲んでいる穴は、すべて面によってふさがれています。そのようなベクトルの集合はまさに\partial_2の像、すなわち\text{Im}\partial_2です。つまり\text{Im}\partial_2の要素はすべて、面によってふさがれている穴を囲んでいるといえるわけです。サイクルの時と同様に、これは\partial_2以外の境界作用素でも考えることができ、\text{Im} \partial_{k+1}のことをkバウンダリーといい、B_k(K)で表します。

サイクルの時と同様に、\partial_2から\text{Im}\partial_1を求めてみましょう。\partial_2は1次元なので、\text{Im}\partial_2と\partial_2は一致します。

\text{Im}\partial_2 = \partial_2 = \begin{pmatrix} 0 \\ 0 \\ 1 \\ -1 \\ 1 \\ 0 \\ 0 \end{pmatrix}

バウンダリーを計算することで、ふさがれている穴を知ることができました。これを先ほどのサイクルから除いたベクトル空間の基底が穴の個数と一致するはずです。

ホモロジー群

ベクトル空間Vから、あるベクトル空間Wの基底を除くことで得られるベクトル空間を商空間といい、V/Wで表します。先ほど説明した通り、穴の個数はサイクルからバウンダリーを除いた空間の基底の個数と一致するので、求めたいのはZ_1/B_1 の次元となります。これを他の次元以外にも拡張して、ある図形Kに対するZ_k(K)/B_k(K)をk次ホモロジー群といい、H_k(K)と表します。穴の数はH_1(K)の次元と一致するということですね。

商空間の次元について、

\text{dim}(V/W) = \text{dim}(V) - \text{dim}(W)

という関係が成り立ちます。1時ホモロジー群の定義は

H_1(K) = Z_1(K)/B_1(K)

なので、求めたいH_1(K)の次元は。

\text{dim}H_1(K) = \text{dim}Z_1(K) - \text{dim}B_1(K)

となります。\text{dim}Z_1(K)と\text{dim}B_1(K)の次元は掃き出し法の要領で求めることができるので、H_1(K)の次元、つまり穴の個数を求めることができます。長い道のりでしたが、やっと穴の個数を求める方法が分かりました。

というわけで、これまで長い道のりを一緒に歩んできてくれたKの穴の個数を計算してみましょう。次元の個数は既定の個数と一致するので、サイクルとバウンダリーの次元はすでに計算されています。

\text{dim}Z_1(K) = 3

\text{dim}B_1(K) = 1

\text{dim}H_1(K) = \text{dim}Z_1(K) - \text{dim}B_1(K) = 2

よってKには穴が2個存在することが確かめられました。

ついでに連結成分の個数も数えてみましょう。今まで穴の個数を数えるためにH_1(K)の次元が穴の個数と一致することを説明してきました。同じように、H_0(K)が連結成分の個数を、H_2(K)が空洞の個数を表しています。よって、連結成分の個数を数えるためには、H_0(K)の次元を計算すればいいことになります。

1単体の境界は存在しないことから、

\text{dim}Z_0(K) = 5

次元定理より、

\text{dim}B_0(K) = 7 - \text{dim}Z_1(K) = 4

よって

\text{dim}H_0(K) = \text{dim}Z_0(K) - \text{dim}B_0(K) = 1

よって連結成分の個数が1個であることが分かりました。

パーシステント図

「やわらかい幾何学１」で「この記事のゴールは、「位相的データ解析」という新しい解析手法にトポロジーがどのように使われているかを知ることです」と言っていました。穴の個数を計算する方法が、どのように応用されているのでしょうか。

点集合が与えられてたとしましょう。最初、各点の半径は0です。これらの点の半径を、時間とともにちょっとづつ大きくしていくことを考えます。すると、あるタイミングでいくつかの点の領域が重なって穴を作る場合があります。同様に、領域が大きくなりすぎて穴が消滅してしまうこともあるでしょう。このように、各点を少しづつ大きくしていくことで、「どのタイミングで穴ができたか」「どのタイミングで穴が消失したか」という情報が得られます。

f:id:Unit112358:20191207234540p:plain

この二つのデータを座標としてグラフにプロットすると、どのくらいの穴があり、それぞれの穴がどのタイミングで出現し、どのタイミングで消滅したかがわかるグラフを作ることができます。このグラフのことをパーシステント図といいます。

f:id:Unit112358:20191207234601p:plain

この図は、点の分布によってさまざまな性質を示します。例えば、ガラスと液体の分子の分布は、人間の見た目では判断しにくいのですが、パーシステント図にすると顕著な違いが現れます。ここでは詳しくは言わないので、気になる人は以下のスライドを見てみてください。

https://www.sci.shizuoka.ac.jp/sciencecafe/news/20160128_02.pdf


他にもパーシステント図を用いた様々な解析方法があります。最近では、機械学習の入力データをトポロジーで生成しようという試みも出てきています。まだまだ発展途上の分野ですが、非常に興味深い分野でもあります。

おわりに

ここまで読んでくださった方、読みにくい文章だったと思いますが、読んでくれてありがとうございました。「やわらかい幾何学１」はともかく、２と３は結構説明が雑になってしまい、申し訳ないと感じています。細かいことを知りたい人はぜひ専門書を読んでみてください。おすすめの専門書を貼っておきます。

www.kyoritsu-pub.co.jp

ちなみに

8記事中4記事を書き終わりました。あと半分です。

やわらかい幾何学２

はじめに

この記事はプログラミングラボ部アドベントカレンダーおかわり部門 7日目の記事として書かれています。

adventar.org

なんかおかわりも順調に埋まっていてすごいですね。

そういえば、この記事は「やわらかい幾何学１」の続きです。

unit112358.hatenablog.com

注意点

この記事には、基本的な群論の知識や、基本的とはいえない線形代数の知識が含まれています。まだそれらを学んでいない、もしくはきちんと理解できていない人は、この記事の内容を理解できない可能性があります。

また、ここからの議論や表現は、分かりやすさを重視するために厳密ではないものになっています。きちんと知りたい人は専門の本を読むか、後日僕に聞きに来てください。

このことを理解したうえで読み進めてください。

前回のおさらい

前回の記事で、トポロジーとは「切り貼りせずに、引っ張ったり伸ばしたりする変形のみで互いに変形可能な図形を同じものとみなす幾何学」であることを説明しました。

そのあと、そのような概念を導入することでどのような利点があるのかをざっくりと説明しました。その中で、トポロジーの利点は「複雑な図形を、同相でもっと単純な別の図形に置き換えることで解析しやすくすることができる」みたいなことを書いたと思います(よく覚えていないのでそうではないかもしれません)。このことについて、具体的な例を交えながら説明していきましょう。

単体複体

目の前に球面があることを想像してみてください。球面なので、球体の表面のみであり、中身は詰まっていないという状態です。球面は、見た目は美しい形をしていますが、頂点も辺もなく、表面は曲がっているので、解析しづらい図形といえます。つかみどころのない図形なのです。

そこで、この球面に対して四方向から圧力をかけて、内部が詰まっていない正四面体にしてみましょう。四方向から縮めただけなので、球面とこの正四面体は同相です。球面よりは、曲線のない四面体の方が解析しやすそうな形をしていますね。トポロジーの世界では同相な二つの図形は同じ性質が成り立つので、この正四面体で成り立つ性質は球面でも成り立つはずです。球面の代わりに正四面体を解析することで、球面の性質を解析してしまおうという魂胆なわけです。
f:id:Unit112358:20191201131229p:plain
正四面体をよく観察してみると、頂点や辺などのいくつかの基本的な図形の組み合わせで作られていることがわかります。四面体は、4個の頂点、6本の辺、そして4つの(三角形の)面からできていることがわかります。
f:id:Unit112358:20191130180457p:plain
どんな三次元の図形も、同相な変形を使って解析しやすい形にすることで、頂点、辺、三角形の面、そして四面体の例では出てきませんでしたが、中身の詰まった四面体、この四つの図形に分解することができます。これらの基本的な図形のことを単体といいます。それぞれの単体には、呼びやすいように別名がついていて、頂点を0単体、辺を1単体、三角形の面を2単体、中身の詰まった四面体を3単体と呼びます。これらの値は各単体の次元に対応しています。
f:id:Unit112358:20191130182710p:plain
逆に、0単体、1単体、2単体、3単体の組み合わせで表現できる図形のことを単体複体といいます。先ほどの例だと、中身の詰まっていない四面体は単体に分解できたので単体複体といえます。逆に、球面はそのままでは単体に分解することができないので単体複体ではありません。トポロジーの利点である解析しやすい図形に置き換えるとは、単体複体に置き換えるということだったわけです。

さて、単体複体に置き換えることで解析しやすくできることが分かりました。次は、解析する方法を紹介していきましょう。

解析の前に

解析の方法を説明するにあたって、実際に図形があったほうが説明も理解もしやすいと思うので、これからの説明の対象となる図形を示しておこうと思います。こちらが、今回の説明の対象になってくれる図形です。以下、この図形のことをKと呼ぶことにします。

f:id:Unit112358:20191205010628p:plain

本当は三次元の図形にしたかったのですが、複雑になると見にくくなるのと、三次元の図形を書くのが面倒くさいので、この簡単な図形を対象にします。最終的に、この図形に1つの連結成分と、2つの穴が存在することを示します。

解析の手始めとして、図形に含まれる各単体を区別できるように名前を付けましょう。つけ方はどのようにしてもいいのですが、今回は画像のように名付けたとして話を進めていきます。頂点はv、辺はe、面はfで表現しています。

鎖群

まずは、単体を代数的に扱う方法を与えます。Kに含まれるk単体に、実数をかけて足し合わせたものの集合をC_k(K)であらわし、k鎖群といいます。言葉だけだと何を言っているかよくわからないと思うので、実際にC_k(K)の要素をいくつか示してみましょう。

C_0(K) \ni \langle v_1 \rangle + 2 \langle v_2 \rangle - \langle v_4 \rangle + 2 \langle v_5 \rangle

C_1(K) \ni \langle e_3 \rangle - \langle e_4 \rangle + \langle e_5 \rangle

こんな感じです。ここで、各単体を\langle \rangleで囲んで見やすくしています。なんて読者思いの人なんだろうと思うかもしれませんが、鎖群はこのように書くのが一般的なだけです。

各単体にかけられている実数は、その単体がいくつ存在しているかを表しています。一つ目の例は、v_1が1個、v_2が2個、v_3が0個、v_4が-1個、v_5が2個あるという状況を表しています。同様に、2つ目の例は、e_1が1個、e_2が-1個、e_3が1個あるという状況を表しています。同じ次元の単体を足し合わせていることに注意してください。こうすることで、どの単体が何個ある、という状況を数式で表せるようになりました。しかし、ここで疑問が生じます。「-1個ある」とはいったいどういう状況なのでしょうか？これは、次に説明する「単体の向き」で説明できます。

各単体に向きを定めます。0単体には向きを付ける必要はありません。1単体についてはどちらの方向を向いているのか、2単体についてはどちらの方向に一周するかを定めていきます。文字だけだとわかりにくいと思いますが、下の図を見るとわかってもらえると思います。e_1はv_1からv_2の方向へ向いていて、f_1は時計回りの方向に一周しています。
f:id:Unit112358:20191205010632p:plain
向きを決めたことで、逆向きの単体を-を付けることで表現できるようになります。\langle e_1 \rangleはv_1からv_2へ向かう辺を表現しているので、- \langle e_1 \rangleはv_2からv_1へ向かう辺を表現していることになります。同じように、- \langle f_1 \rangleは反時計回りのf_1を表現します。鎖群の二つ目の例で、e_2が-1個あるということを表現していましたが、これはe_2とは逆向きの辺が1個ある、ということを表現していたわけです。このことからわかる重要なこととして、ある単体と、その単体とは逆向きの単体を代数的にまとめて表現すると、打ち消しあって0になることがわかります。例えば、e_3と逆向きのe_3を代数的にまとめて表現すると、

\langle e_3 \rangle - \langle e_3 \rangle = 0

となって打ち消します。

境界

続いて境界を定義します。簡単な定義は以下のようになると思います。

ある鎖群の要素を囲んでいる単体に、適切に+か-をつけて足し合わせて作られる鎖群を、元の鎖群の境界という。

言葉だと非常に説明しづらい概念なので、いつもどおり図を使って説明していきましょう。f_1に注目してみましょう。f_1はe_3、e_4、e_5の3つの0単体に囲まれています。このとき、e3に+を、e4に-を、e5に+をつけて足しあわせたもの、すなわち\langle e_3 \rangle - \langle e_4 \rangle + \langle e_5 \rangleがf_1の境界になります。
f:id:Unit112358:20191204184618p:plain
囲まれている、という意味は図を見ればなんとなく理解できると思います。しかし、+と-の符号はどうやって求めるのでしょうか。実は、これらの実数の求め方は鎖群の次元によって異なっているので、どの次元にも成り立つような決め方はありません。というわけで、各次元での求め方を順に説明していきましょう。

以下の説明でxの境界がyの時、\partial (x) = yと表現しています。\partialについては後ほど詳しく説明するので、今は境界を計算する関数のようなものであると考えておいてください。

C_0(K)

C_0(K)の要素の境界は0です。どんな要素をとってきても、その境界は0であると定義されています。いくつか例を示しましょう。

\partial(\langle v_1 \rangle + \langle v_3 \rangle) = 0

\partial(\langle v_4 \rangle + 2 \langle v_5 \rangle) = 0

このように、どんなC_0(K)の要素の境界も0となります。数式であらわされている状況を図形で見てみましょう。
f:id:Unit112358:20191205010644p:plain
これは「C_0(K)に境界は存在しない」というふうにも解釈することができます。

C_1(K)

C_1(K)の要素の境界は、各1単体がどの0単体からどの0単体に向かっているかによって変わります。v_aからv_bへ向かうような1単体の境界は、 - \langle v_a \rangle + \langle v_b \rangle と定義されます。先ほどと同じように、いくつか例を示しましょう。各単体の向きやつながり方はKと揃えてあります。わざわざ戻って確認するのは面倒だと思うので、再登場してもらいましょう。図形のKさんです。
f:id:Unit112358:20191205010632p:plain
\partial (\langle e_1 \rangle) = - \langle v_1 \rangle + \langle v_2 \rangle

\partial (2\langle e_2 \rangle - \langle e_4 \rangle) = 2(-\langle v_3 \rangle + \langle v_1 \rangle) - (-\langle v_2 \rangle + \langle v_5 \rangle) = 2\langle v_1 \rangle + \langle v_2 \rangle -2 \langle v_3 \rangle - \langle v_5 \rangle

\partial (\langle e_1 \rangle + \langle e_2 \rangle + \langle e_3 \rangle) = (-\langle v_1 \rangle + \langle v_2 \rangle) + (-\langle v_3 \rangle + \langle v_1 \rangle) + (-\langle v_2 \rangle + \langle v_3 \rangle) = 0

ごちゃごちゃしていてわかりにくいですね。順に説明していきましょう。

１つ目の例はe_1の境界を計算しています。e_1はv_1からv_2へ向かっているので、e_1の境界は - \langle v_1 \rangle + \langle v_2 \rangleとなります。

２つ目の例は2\langle e_2 \rangle - \langle e_4 \rangleの境界を計算しています。この例では、まず2\langle e_2 \rangle - \langle e_4 \rangleを2\langle e_2 \rangleと- \langle e_4 \rangleに分けて、二つの計算結果を最後に足し合わせていることがわかります。それぞれの計算はどうなっているでしょうか。2\langle e_2 \rangleの計算では、まず\langle e_2 \rangleの境界を計算して、後から2を全体にかけていることがわかります。

ちなみに、-が付いた単体は逆向きを表すという話をしましたが、-が付いた単体の境界を計算をするときは、逆向きの単体の境界を求めても、そのままの単体の境界をもとめて最後に-をかけても、同じ結果になります。
f:id:Unit112358:20191205010647p:plain
この例から、\partialには

\partial (x+y) = \partial(x) + \partial(y)

\partial(ax) = a\partial(x)

この二つの性質が成り立っていることがわかります。いわゆる線形性というやつですね。

３つ目の例は非常に重要です。\langle e_1 \rangle + \langle e_2 \rangle + \langle e_3 \rangleの境界を計算しています。これも２つ目の例と同じように、線形性を使って計算を進めていくのですが。出てきた式を整理すると+と-が打ち消しあって0になっていることがわかります。これは下の図を見てもらうと何が起きているのか分かりやすいでしょう。
f:id:Unit112358:20191205010656p:plain
つまり、それぞれの1単体をつなげると、ある方向にぐるっと一周するわっかになる場合、その境界は打ち消しあって0になります。後ほど、この性質が穴がいくつあるかを調べるための手掛かりとなります。

C_2(K)

C_2(K)の要素の境界は、各2単体どの方向に一周しているかと、まわりの1単体がどの方向を向いているかで決まります。周りの1単体のうち、2単体の回転方向と同じ向きを向いているものには+を、そうでないものには-を付けて足し合わせます。例によって、例を示しましょう。

\partial(\langle f_1 \rangle)= \langle e_3 \rangle - \langle e_4 \rangle + \langle e_5 \rangle

f_1の回転方向とe_3の向いている方向を比べてみましょう。どちらも時計回り方向を向いています。先ほど言ったように、同じ方向を向いているのでe_3には+を付けます。e_4はどうでしょうか。先ほどとは違い逆方向を向いています。よって、e_4には-を付けます。最後にe_5を見てみると、同じ方向を向いているので+を付ければよいことがわかります。これらを足し合わせることで\langle e_3 \rangle - \langle e_4 \rangle + \langle e_5 \rangleとなります。
f:id:Unit112358:20191205010709p:plain
さて、ここで計算した結果でてきた境界、つまり\langle e_3 \rangle - \langle e_4 \rangle + \langle e_5 \rangleの方に注目してみましょう。図形的にみると、ぐるっと一周している1単体の集まりであることがわかります。C_1(K)の時に話したように、ぐるっと一周しているわっかの境界は0になるのでした。すなわち\partial(\langle e_3 \rangle - \langle e_4 \rangle + \langle e_5 \rangle) = 0となるわけです。これらをまとめると、

 \partial(\partial(\langle f_1 \rangle)) = \partial(\langle e_3 \rangle - \langle e_4 \rangle + \langle e_5 \rangle)) = 0

となります。ここで、一番左の式と一番右の式に注目すると

\partial(\partial(\langle f_1 \rangle)) = 0

つまり \langle f_1 \rangleから2回境界を計算すると0になるということがわかります。この性質はf_1だけではなく、どんなC_k(K)の要素に対しても成り立ちます。すなわち、

任意のk \in C_k(K)について\partial(\partial(k)) = 0

が成り立ちます。これも非常に重要な性質なので、気になる人は計算して確かめてみてください。(本当は証明を載せたいんですが、これまでの議論が厳密ではないので厳密な証明ができないんですよね。悲しい)

境界作用素

では、境界のところで後回しにしていた\partialの説明をしていきましょう。

まず\partialの定義域と値域を考えてみましょう。以下の図のように、\partialはC_2(K)をC_1(K)に、C_1(K)をC_0(K)に、そしてC_0(K)を0に移していました。
f:id:Unit112358:20191205010720p:plain
C_k(K)の要素は同じ次元の単体に実数を欠けて足し合わせたものでした。それぞれの単体を変数としてみると、多元一次方程式とみなすことができます。さらに、多元一次方程式の各係数を要素と持つようなベクトルを考えることで、多元一次方程式をベクトルと同一視することができるようになります。
f:id:Unit112358:20191205115714p:plain
このような見方をすることで、\partialはベクトルをベクトルに移すような線形写像、つまり行列であると考えることができます。ただし、ベクトルの次元(単体の次元ではなく単体の個数)は異なっている可能性があるため、これまでのように\partialひとつで変換を表すことはできません。ということで、それぞれの次元(こっちは単体の次元です)に対応する写像を用意します。C_k(K)に対応するベクトルを、C_{k-1}(K)に対応するベクトルに移す線形写像を\partial_kとあらわし、境界作用素といいます。
f:id:Unit112358:20191205115813p:plain
理論の話ばかりで想像しにくいと思うので、ひとつ計算例を示しましょう。境界の説明のところで

\partial (2\langle e_2 \rangle - \langle e_4 \rangle) = 2\langle v_1 \rangle + \langle v_2 \rangle -2 \langle v_3 \rangle - \langle v_5 \rangle

という計算をしたと思います。これを境界作用素の考え方で置き換えるとどのようになるでしょうか。まず、境界を計算する対象をベクトルとして表現します。ベクトルの第1要素を \langle e_1 \rangle、第7要素を \langle e_7 \rangleに対応させると、以下のように置き換えることができます。

2\langle e_2 \rangle - \langle e_4 \rangle \mapsto \begin{pmatrix} 0 \\ 2 \\ 0 \\ -1 \\ 0 \\ 0 \\ 0 \end{pmatrix}

同じように、境界の方も置き換えてみましょう。

2\langle v_1 \rangle + \langle v_2 \rangle -2 \langle v_3 \rangle - \langle v_5 \rangle \mapsto \begin{pmatrix} 2 \\ 1 \\ -2 \\ 0 \\ -1 \end{pmatrix}

2\langle e_2 \rangle - \langle e_4 \rangleはC_1(K)の要素なので、\partial_1が対応します。よって

\partial_1 \begin{pmatrix} 0 \\ 2 \\ 0 \\ -1 \\ 0 \\ 0 \\ 0 \end{pmatrix} = \begin{pmatrix} 2 \\ 1 \\ -2 \\ 0 \\ -1 \end{pmatrix}

という計算が成り立つような\partial_1が一次元の境界作用素となるのです。

では、境界作用素はどのように求めればいいのでしょうか。例えば\partial_1を求めたい場合、各1単体について \langle e_1 \rangleから順に境界を計算し、その結果をベクトルに変換したものを左から右へ並べるだけで求めることができます。
f:id:Unit112358:20191205115742p:plain
この方法で求めた\partial_2、\partial_1、\partial_0は以下のようになります。

\partial_2 = \begin{pmatrix} 0 \\ 0 \\ 1 \\ -1 \\ 1 \\ 0 \\ 0 \end{pmatrix}

\partial_1 = \begin{pmatrix} -1 & 1 & 0 & 0 & 0 & 0 & 0 \\ 1 & 0 & -1 & -1 & 0 & 0 & 0 \\ 0 & -1 & 1 & 0 & -1 & -1 & 0 \\ 0 & 0 & 0 & 0 & 0 & 1 & -1 \\ 0 & 0 & 0 & 1 & 1 & 0 & 1 \end{pmatrix}

\partial_0 = \begin{pmatrix} 0 & 0 & 0 & 0 & 0 \end{pmatrix}

せっかく求めたので、これらを使って境界を計算することができるかどうか確かめてみましょう。先ほど

\partial_1 \begin{pmatrix} 0 \\ 2 \\ 0 \\ -1 \\ 0 \\ 0 \\ 0 \end{pmatrix} = \begin{pmatrix} 2 \\ 1 \\ -2 \\ 0 \\ -1 \end{pmatrix}

という式をだしました、\partial_1を代入すると、

\begin{pmatrix} -1 & 1 & 0 & 0 & 0 & 0 & 0 \\ 1 & 0 & -1 & -1 & 0 & 0 & 0 \\ 0 & -1 & 1 & 0 & -1 & -1 & 0 \\ 0 & 0 & 0 & 0 & 0 & 1 & -1 \\ 0 & 0 & 0 & 1 & 1 & 0 & 1 \end{pmatrix} \begin{pmatrix} 0 \\ 2 \\ 0 \\ -1 \\ 0 \\ 0 \\ 0 \end{pmatrix} = \begin{pmatrix} 2 \\ 1 \\ -2 \\ 0 \\ -1 \end{pmatrix}

となります。計算してみるとわかると思いますが、ちゃんと成り立っていますね。このように、境界作用素を適用するだけで境界を求めることができるようになります。

境界作用素を求めたことで、トポロジー的な解析をするために必要な道具はすべてそろいました。これでやっと解析へ踏み込むことができます。

お詫び

道具がそろって解析する気満々の人が多いと思いますが、すでに「やわらかい幾何学１」の2倍を超える文字数になっているため、読みにくくならないように記事を分けることにしました。

続きが気になる方は「やわらかい幾何学３」をお読みください。

https://unit112358.hatenablog.com/entry/2019/12/07/000009?_ga=2.253468041.1411535617.1575556889-1110943558.1498307490

おススメのYoutuberの紹介

この記事は、プログラミングラボ部アドベントカレンダー2019趣味部門 ６日目の記事として書かれています。

adventar.org

8個も記事を書くのはつらいですね。

はじめに

やわらかい幾何学を書くのはかなり時間をかけたのですが、他の記事は適当に書こうと思っているのでそんなに面白くないです。

おすすめのYoutuberの紹介

3Blue1Brown

Youtubeに数学系の解説動画を上げている方です。

www.youtube.com

解説している分野は線形代数、微積、ニューラルネットワーク、フーリエ変換など多岐にわたり、そのすべてで本質的な知識を分かりやすい動画付きで解説しています。僕の数学的な知識はほぼこの人の動画から得たものです。

3Blue1Blownの動画の中で最初に見たのは、Essence of linear algebra(線形代数の本質)というシリーズで、三年生までのベクトルや行列の知識があいまいだった僕にとってはかなり衝撃的な動画でした。

www.youtube.com


そのあとも、krk先生の応用数学１でフーリエ変換がよく理解できていなかったときに、フーリエ変換を視覚的に解釈する方法を紹介している動画を見て、とても理解が深まった覚えがあります。

www.youtube.com

他の動画も、数学を使った技術の解説や、数学関連の面白いトピックなど、様々な動画があるのでぜひ見てください。

ただし、動画はすべて英語で解説されているので、英語がわからない人は日本語の字幕に頼る必要があります(僕もお世話になっていました)。最近の自動翻訳の精度はかなり高いので、おそらく問題なく見ることができると思います。英語の勉強にもなると思うのでぜひ見ましょう。

MKR

こちらはゲームの実況動画を上げている方です。

www.youtube.com

昔はニコニコ動画で活動していた方なのですが、一年前ほど前からYoutubeでも活動を開始しました。最近はゲームの実況動画などはほとんど見ない僕ですが、この方の動画は見ています。少し古めのゲームから最新のゲームまで、様々なゲームを実況していて、ゲーム以外にも実写動画や歌ってみたなどが時々投稿されています。

www.youtube.com

おススメの動画です。

個人的にとても面白いと思うので、興味がある人は暇な時間に見てみてください。

また、この方の動画はすべて日本語なので、日本語以外の言語がわからない人でも安心してみることができます。うれしいですね。

おわり

明日はみやこらたさんの記事です。お皿を回すようですね。

おまけ

垢ハックには気を付けましょう。

f:id:Unit112358:20191205234545p:plain

ちなみに上の方は本音です。共感できる人は「杜野凛世」と検索しましょう。

やわらかい幾何学１

はじめてのアドベントカレンダー

この記事はプログラミングラボ部アドベントカレンダープロ部門 2日目の記事として書かれています。

https://adventar.org/calendars/4410

ブログはおろか、こういった記事を書くのは初めてのことですので、読みにくい文章になってしまうかもしれませんがご了承ください。

初めに

今年から、四年生のカリキュラムにリベラルアーツ特論というものが追加されました。これは、各生徒がいくつかの分野から好きなものを選んで、同じ分野を選んだ生徒と一緒に一年間勉強する、というものです。

僕はトポロジーという分野を選びました。理由は今まで聞いたことのない分野だったので、興味がわいたからです。半年とちょっとのあいだ、この分野をを勉強してきて、結構面白い分野であることがわかったので記事にしたいと思います。

目標

この記事のゴールは、「位相的データ解析」という新しい解析手法にトポロジーがどのように使われているかを知ることです。何のことかよくわからないと思いますが、この記事を読み終わったころには、何となくどんなものか分かっていることを目指します。

では、さっそく説明を始めていきましょう。

やわらかい幾何学

トポロジーはしばしば、「やわらかい幾何学」と表現されることがあります。どうしてそのような表現が使われるのか、まずはそこから話を始めたいと思います。

我々がなじみ深いユークリッド幾何学には、合同という概念があります(記号は\equiv)。ご存じの通り(ご存じでない人もいるかもしれませんが)形と大きさが等しい二つの図形は合同である、と表現されます。合同であるような図形は同じものとして扱われ、同じ性質が成り立ちます。

f:id:Unit112358:20191126145536p:plain

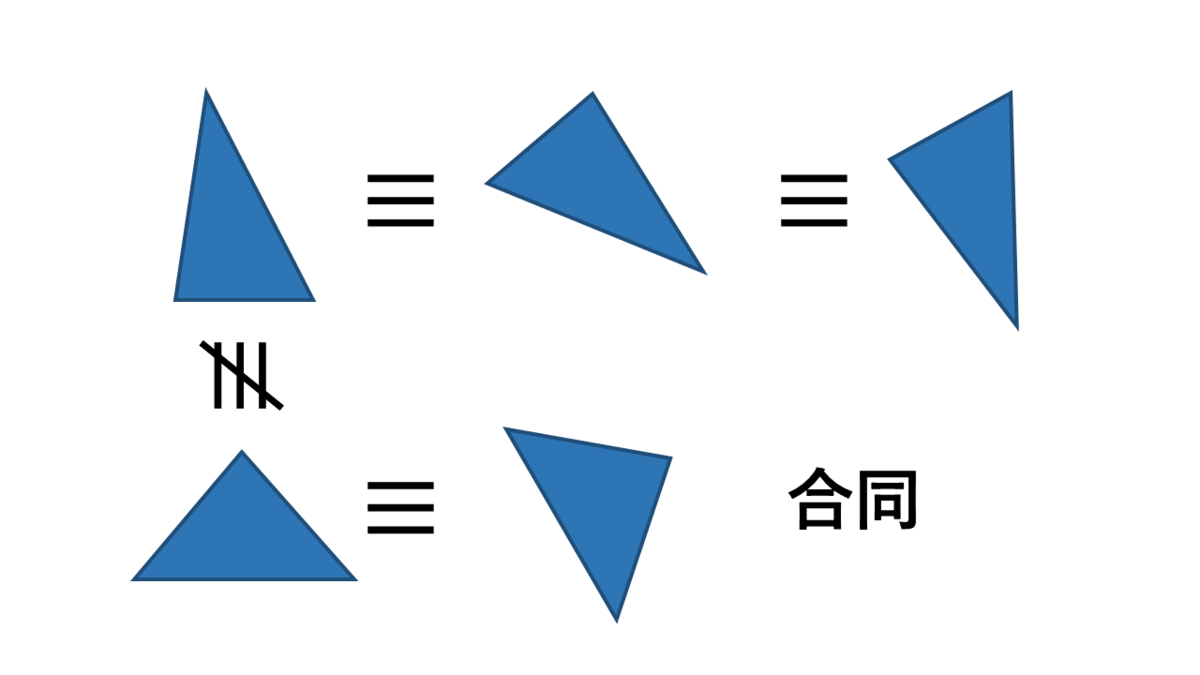
トポロジーには合同の代わりに、同相という概念があります(記号は\simeq)。トポロジーの世界では、同相な二つの図形は同じものとして扱われ、同じ性質が成り立ちます。定義は以下の通りです。

図形Aと図形A'があり、A上の点をA'に移す1対1の対応であって、その対応と逆対応がともに連続であるようなものが存在するとき、AとA'は同相である。

何やらよくわからないことを言われて嫌な気持ちになりますね。文章だけではイメージしづらいので、図を使って説明しましょう。

同相とは？

ここに輪ゴムがあるとします(もし用意できる人は実際に動かしながら考えてみましょう)。今、輪ゴムは細い線でできた輪のようなものだと考えることができます。輪ゴムを三方向から引っ張って三角形を作ってみましょう。

f:id:Unit112358:20191126151843p:plain変形前の輪ゴムと変形後の輪ゴムは同相です。このことを確かめてみましょう。同相かどうかを確かめるには以下の2つのことを確かめる必要があります。

  1. 変形前の輪ゴムと変形後の輪ゴムが、一対一の関係を満たしていること。
  2. その対応が連続であり、その逆対応も連続であること。

1.については簡単です。変形前の輪ゴム上の一点を適当にとってきます。その点に視点を合わせながら、輪ゴムを三角形に変形させると、その点は変形後の輪ゴム上の一点に移ります。同じように、さっきとは違う一点を適当にとってきて、その点を眺めながら変形させると、先ほどとは違う一点へ移ります。このように、変形前の輪ゴム上の一点は、変形後の輪ゴム上の一点と一対一の関係があります。

f:id:Unit112358:20191126155549p:plain

2.についてはどうでしょうか？今、変形前の輪ゴム上の一点aが変形後の輪ゴム上の一点a'に移ったとします。ここで、aのすぐ近くにあるbが、変形後の輪ゴム上の一点b'に移ったとしましょう。この時、aとbと同じように、a'とb'もすぐ近くにあります。このように、変形前の輪ゴム上で近くにあった二つの点は、変形後の輪ゴム上でも近くにあります。よって、この変形は連続であることがわかります。

f:id:Unit112358:20191130123548p:plain

これらのことから、変形前の輪ゴムと変形後の輪ゴムは同相であることが分かりました。

次に同相ではない例を紹介します。成り立つ例のみを説明されても、成り立たない例を説明されないと区別しづらいですからね。

 輪ゴムをすごい力で押し縮めて、一点に凝縮したとしましょう(ただ小さくしたのではなく、0次元の点に押し縮めます)。この時、変形前の輪ゴムと変形後の輪ゴムは同相ではありません。変形前の輪ゴム上の任意の点は、すべて変形後の一点へと移ります。これでは一対一の関係ではなく、多対一の関係になってしまうため、1.の条件を満たしていません。よって、変形前と変形後の輪ゴムは同相ではないことがわかります。

f:id:Unit112358:20191129154409p:plain

輪ゴムをすごい力で引き延ばし、引きちぎってしまった場合はどうでしょうか？変形後の輪ゴムは一本の線のように見なすことができるようになります(もはや輪ゴムではありませんね)。この場合は一対一の関係は満たされています。ここで、変形後の輪ゴムの両端の２点に注目してみましょう。これらの点は、変形前の輪ゴム上ではすぐ近くにありましたが、変形後の輪ゴムでは離れたところにあります。これでは連続な対応とは言えないので、2.の条件を満たしていません。よって、変形前の輪ゴムと変形後の輪ゴムは同相ではないことが分かります。

f:id:Unit112358:20191129155831p:plain

長々と同相の例を書いてきましたが、直感的には「切り貼りせずに、伸び縮みさせることで互いに変形させることができる図形は同相な関係にある」といえます。輪ゴムの例では2次元での同相でしたが、同じように1次元や、3次元、それ以上の次元でも同じように同相が定義されます。wikipediaの動画では、ドーナツと、取っ手のついたマグカップが同相であることを視覚的に確認することができます。イメージがつかない人は見てみてください。https://ja.wikipedia.org/wiki/%E4%BD%8D%E7%9B%B8%E5%90%8C%E5%9E%8B

f:id:Unit112358:20191130133745p:plain

さて、これまでトポロジーが「伸び縮みさせてたがいに変形させることができる図形を同じものとみなす幾何学」であることを説明してきました。これはまるで、粘土のような変形しやすいやわらかい物質に対して、様々な変形を加えながら、どのような性質を持っているのかを調べる学問だとみなすことができます。これがトポロジーが「やわらかい幾何学」と呼ばれている理由です。

利点と欠点

しかし、変形させてしまっては元の図形にあった様々な性質が失われてしまうのではないでしょうか？解析したい図形の性質が変わってしまっては元も子もありません。では一体、何のために同相という考え方を導入したのでしょうか？そういった疑問に答えるために、トポロジーがユークリッド幾何学に比べて、どのような利点と欠点を持っているのかを説明しましょう。

欠点

まず欠点についてです。同相な変形をすることによって、一部の性質が失われてしまうのは間違いありません。長さや角度などがその例です。そのため、長さや角度に基づいた解析をしたい場合には、トポロジーは使えません。建築家が、全く大きさの違う二つの建物を建てて「この二つの建物は同相だから同じもの、だから同じ値段で売る」なんて言い出したら困りますよね。

しかし、同相な図形どうしで不変なものもあります。例えば、連結成分の個数は変わりません。1つのボールを伸び縮みさせて2つのボールに分かれることはありませんし、複数の図形が1つにまとまることもありません。また、穴の数も不変です。wikipediaの動画にあるように、ドーナツと1つの取っ手が付いたコップは同相です。どちらも1つの穴が開いています。これらに変形を加えることで、穴をなくしたり、穴を増やしたりすることはできません。このように、同相な図形どうしで不変なもののことを不変量といいます。トポロジーは、同相に関する不変量を調べる幾何学であるといえます。

f:id:Unit112358:20191130141733p:plain

先ほど挙げたような不変量のみからわかることは何でしょうか？例えば、ある物質をトポロジーで解析した結果、たくさんの穴が開いていることがわかったとしましょう。すると、この物質は水を通しやすいのではないか、という予想がつきます。同じように、たくさんの空洞(空洞の個数も不変量です)があることがわかれば、その物質がやわらかいのではないかと予想がつきます。このように、長さなどに基づいた厳密な解析はできませんが、物質の性質を予測したり、分類したりすることができるのです。

利点

では、同相という概念を使うことでえられる利点は何でしょうか？それは「複雑な図形を、同相でもっと単純な図形に置き換えることで、解析がしやすくなる」というものです。このことについてここから書いていってもいいのですが、記事が長くなりすぎるのと、これからの内容は少々高度な内容になるので記事を分けようと思います。

終わりに

ここまでの記事で満足できたという人は、ここで読むのをやめてしまっても構いません。普段見ているものの見方とは違ったものの見方があることを知ってもらえたとしたら、それだけで僕は満足です。

トポロジーがどのように応用されているのかを知りたい人は、この記事の続きである「やわらかい幾何学２」を覗いてみてください。

https://unit112358.hatenablog.com/entry/2019/12/07/000009?_ga=2.253468041.1411535617.1575556889-1110943558.1498307490

明日はTuranさんの記事です。どうやら数学関係の記事のようなので、数学続きになりそうですね。楽しみです。

豆知識

今回が初めてのアドベントカレンダーだということを最初にお話ししました。せっかくアドベントカレンダーを書くので、複数の記事を書きたいと思って、プロラボのMisskeyでこんな投稿をしてみました。

f:id:Unit112358:20191130134248p:plain

上の画像では10個リアクションがついていますが、僕が締め切った後に2個付いたので、合計8個の記事を書く羽目になっています。皆さんもこういった投稿をする際には、最悪の場合どのようなことになるのかを想定したうえでやりましょう。