やわらかい幾何学1
はじめてのアドベントカレンダー
この記事はプログラミングラボ部アドベントカレンダープロ部門 2日目の記事として書かれています。
https://adventar.org/calendars/4410
ブログはおろか、こういった記事を書くのは初めてのことですので、読みにくい文章になってしまうかもしれませんがご了承ください。
初めに
今年から、四年生のカリキュラムにリベラルアーツ特論というものが追加されました。これは、各生徒がいくつかの分野から好きなものを選んで、同じ分野を選んだ生徒と一緒に一年間勉強する、というものです。
僕はトポロジーという分野を選びました。理由は今まで聞いたことのない分野だったので、興味がわいたからです。半年とちょっとのあいだ、この分野をを勉強してきて、結構面白い分野であることがわかったので記事にしたいと思います。
目標
この記事のゴールは、「位相的データ解析」という新しい解析手法にトポロジーがどのように使われているかを知ることです。何のことかよくわからないと思いますが、この記事を読み終わったころには、何となくどんなものか分かっていることを目指します。
では、さっそく説明を始めていきましょう。
やわらかい幾何学
トポロジーはしばしば、「やわらかい幾何学」と表現されることがあります。どうしてそのような表現が使われるのか、まずはそこから話を始めたいと思います。
我々がなじみ深いユークリッド幾何学には、合同という概念があります(記号は)。ご存じの通り(ご存じでない人もいるかもしれませんが)形と大きさが等しい二つの図形は合同である、と表現されます。合同であるような図形は同じものとして扱われ、同じ性質が成り立ちます。
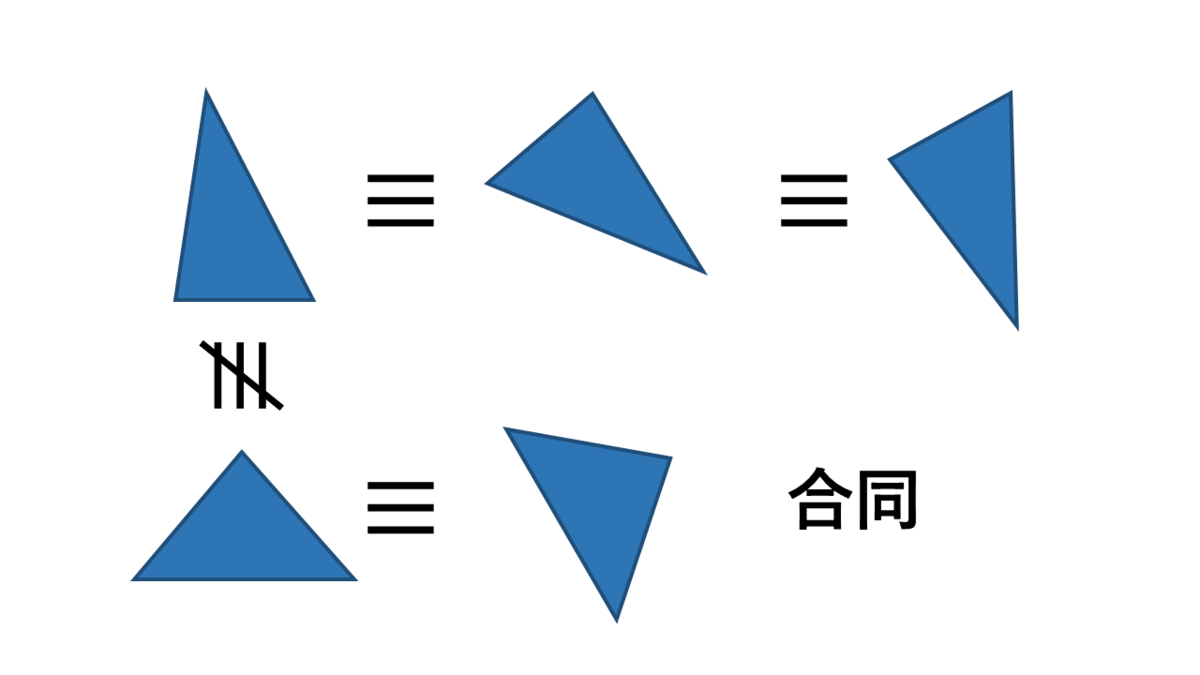
トポロジーには合同の代わりに、同相という概念があります(記号は)。トポロジーの世界では、同相な二つの図形は同じものとして扱われ、同じ性質が成り立ちます。定義は以下の通りです。
図形と図形
があり、
上の点を
に移す1対1の対応であって、その対応と逆対応がともに連続であるようなものが存在するとき、
と
は同相である。
何やらよくわからないことを言われて嫌な気持ちになりますね。文章だけではイメージしづらいので、図を使って説明しましょう。
同相とは?
ここに輪ゴムがあるとします(もし用意できる人は実際に動かしながら考えてみましょう)。今、輪ゴムは細い線でできた輪のようなものだと考えることができます。輪ゴムを三方向から引っ張って三角形を作ってみましょう。
 変形前の輪ゴムと変形後の輪ゴムは同相です。このことを確かめてみましょう。同相かどうかを確かめるには以下の2つのことを確かめる必要があります。
変形前の輪ゴムと変形後の輪ゴムは同相です。このことを確かめてみましょう。同相かどうかを確かめるには以下の2つのことを確かめる必要があります。
- 変形前の輪ゴムと変形後の輪ゴムが、一対一の関係を満たしていること。
- その対応が連続であり、その逆対応も連続であること。
1.については簡単です。変形前の輪ゴム上の一点を適当にとってきます。その点に視点を合わせながら、輪ゴムを三角形に変形させると、その点は変形後の輪ゴム上の一点に移ります。同じように、さっきとは違う一点を適当にとってきて、その点を眺めながら変形させると、先ほどとは違う一点へ移ります。このように、変形前の輪ゴム上の一点は、変形後の輪ゴム上の一点と一対一の関係があります。

2.についてはどうでしょうか?今、変形前の輪ゴム上の一点が変形後の輪ゴム上の一点
に移ったとします。ここで、
のすぐ近くにある
が、変形後の輪ゴム上の一点
に移ったとしましょう。この時、
と
と同じように、
と
もすぐ近くにあります。このように、変形前の輪ゴム上で近くにあった二つの点は、変形後の輪ゴム上でも近くにあります。よって、この変形は連続であることがわかります。

これらのことから、変形前の輪ゴムと変形後の輪ゴムは同相であることが分かりました。
次に同相ではない例を紹介します。成り立つ例のみを説明されても、成り立たない例を説明されないと区別しづらいですからね。
輪ゴムをすごい力で押し縮めて、一点に凝縮したとしましょう(ただ小さくしたのではなく、0次元の点に押し縮めます)。この時、変形前の輪ゴムと変形後の輪ゴムは同相ではありません。変形前の輪ゴム上の任意の点は、すべて変形後の一点へと移ります。これでは一対一の関係ではなく、多対一の関係になってしまうため、1.の条件を満たしていません。よって、変形前と変形後の輪ゴムは同相ではないことがわかります。

輪ゴムをすごい力で引き延ばし、引きちぎってしまった場合はどうでしょうか?変形後の輪ゴムは一本の線のように見なすことができるようになります(もはや輪ゴムではありませんね)。この場合は一対一の関係は満たされています。ここで、変形後の輪ゴムの両端の2点に注目してみましょう。これらの点は、変形前の輪ゴム上ではすぐ近くにありましたが、変形後の輪ゴムでは離れたところにあります。これでは連続な対応とは言えないので、2.の条件を満たしていません。よって、変形前の輪ゴムと変形後の輪ゴムは同相ではないことが分かります。

長々と同相の例を書いてきましたが、直感的には「切り貼りせずに、伸び縮みさせることで互いに変形させることができる図形は同相な関係にある」といえます。輪ゴムの例では2次元での同相でしたが、同じように1次元や、3次元、それ以上の次元でも同じように同相が定義されます。wikipediaの動画では、ドーナツと、取っ手のついたマグカップが同相であることを視覚的に確認することができます。イメージがつかない人は見てみてください。https://ja.wikipedia.org/wiki/%E4%BD%8D%E7%9B%B8%E5%90%8C%E5%9E%8B

さて、これまでトポロジーが「伸び縮みさせてたがいに変形させることができる図形を同じものとみなす幾何学」であることを説明してきました。これはまるで、粘土のような変形しやすいやわらかい物質に対して、様々な変形を加えながら、どのような性質を持っているのかを調べる学問だとみなすことができます。これがトポロジーが「やわらかい幾何学」と呼ばれている理由です。
利点と欠点
しかし、変形させてしまっては元の図形にあった様々な性質が失われてしまうのではないでしょうか?解析したい図形の性質が変わってしまっては元も子もありません。では一体、何のために同相という考え方を導入したのでしょうか?そういった疑問に答えるために、トポロジーがユークリッド幾何学に比べて、どのような利点と欠点を持っているのかを説明しましょう。
欠点
まず欠点についてです。同相な変形をすることによって、一部の性質が失われてしまうのは間違いありません。長さや角度などがその例です。そのため、長さや角度に基づいた解析をしたい場合には、トポロジーは使えません。建築家が、全く大きさの違う二つの建物を建てて「この二つの建物は同相だから同じもの、だから同じ値段で売る」なんて言い出したら困りますよね。
しかし、同相な図形どうしで不変なものもあります。例えば、連結成分の個数は変わりません。1つのボールを伸び縮みさせて2つのボールに分かれることはありませんし、複数の図形が1つにまとまることもありません。また、穴の数も不変です。wikipediaの動画にあるように、ドーナツと1つの取っ手が付いたコップは同相です。どちらも1つの穴が開いています。これらに変形を加えることで、穴をなくしたり、穴を増やしたりすることはできません。このように、同相な図形どうしで不変なもののことを不変量といいます。トポロジーは、同相に関する不変量を調べる幾何学であるといえます。

先ほど挙げたような不変量のみからわかることは何でしょうか?例えば、ある物質をトポロジーで解析した結果、たくさんの穴が開いていることがわかったとしましょう。すると、この物質は水を通しやすいのではないか、という予想がつきます。同じように、たくさんの空洞(空洞の個数も不変量です)があることがわかれば、その物質がやわらかいのではないかと予想がつきます。このように、長さなどに基づいた厳密な解析はできませんが、物質の性質を予測したり、分類したりすることができるのです。
利点
では、同相という概念を使うことでえられる利点は何でしょうか?それは「複雑な図形を、同相でもっと単純な図形に置き換えることで、解析がしやすくなる」というものです。このことについてここから書いていってもいいのですが、記事が長くなりすぎるのと、これからの内容は少々高度な内容になるので記事を分けようと思います。
終わりに
ここまでの記事で満足できたという人は、ここで読むのをやめてしまっても構いません。普段見ているものの見方とは違ったものの見方があることを知ってもらえたとしたら、それだけで僕は満足です。
トポロジーがどのように応用されているのかを知りたい人は、この記事の続きである「やわらかい幾何学2」を覗いてみてください。
明日はTuranさんの記事です。どうやら数学関係の記事のようなので、数学続きになりそうですね。楽しみです。
豆知識
今回が初めてのアドベントカレンダーだということを最初にお話ししました。せっかくアドベントカレンダーを書くので、複数の記事を書きたいと思って、プロラボのMisskeyでこんな投稿をしてみました。

上の画像では10個リアクションがついていますが、僕が締め切った後に2個付いたので、合計8個の記事を書く羽目になっています。皆さんもこういった投稿をする際には、最悪の場合どのようなことになるのかを想定したうえでやりましょう。